| |
Subjecting
a material to a hydrostatic stress also causes elastic deformation. The
stress is the pressure, p,
acting on the body and the strain, d
= DV/V. These quantities are related
through a Hookian relationship involving the "Bulk modulus," K: p = Kd.
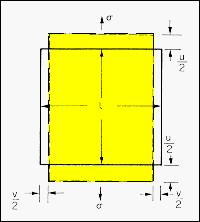
A final elastic constant is Poisson's
ratio, n. This is the ratio of the
longitudinal to transverse strains in a body subjected to a uniaxial stress
and is given by: n = -(lateral strain/tensile strain). For the sample shown
in the lower diagram,
n = - (v/L)/(u/L) = -(v/u).
Many
materials have isotropic elastic properties and consequently there are
relationships linking the elastic constants discussed. For these isotropic
materials, only two independent elastic constants are required and E, and n,
are normally selected due to the facility with which they can be measured.
The relations linking these constants to the others are given below.
E = 2G(1
+ n), G = E/2(1 + n), K = E/3(1 + 2n).
Values
for these elastic constants will be required to select a material for
a structural task. |
|
|
|
|
|
|
|
|
|
|
|
|
|